汽车数据线缆探讨之特性抗阻篇
所属分类: 行业动态 发布时间:2023-10-06
随着汽车ADAS的发展,对车载数据传输速率要求越来越高,想要高速信号传输,必须要更精准的特性阻抗。所以,汽车数据线缆公司对于特性阻抗的严格管控至关重要!今天我们就来探讨一下汽车数据线缆特性阻抗的话题。
汽车数据线缆第一指标要求就是特性阻抗,这个特性阻抗是什么意思呢?
在谈特性阻抗之前,我们首先要确定一个概念,信号在传输线中,是一步一步向前走的,电磁场的建立也是需要一个过程的,信号不是一下子从发射端传播到接收端。
信号每向前传播一步都会遇到特定的电容参数与电感参数,这里我们引入两个新的变量:“单位长度电容C”与“单位长度电感L”。
特性阻抗不是个基础概念,而是应用于传输线的概念。在高速应用场景,信号传输线已经不能看作理想导线,不能忽略传输线上的一些寄生参数,如寄生电阻、寄生电容、寄生电感。特性阻抗就是一个综合传输线场景下这些参数的合成参数。
单位长度的传输线可以等效为以下模型(如图1所示):
信号每走一步都会遇到C和L,此时的特性阻抗定义为(如图2a所示),理论上精确的特性阻抗是一个与频率相关的量。而在实际应用中,传输线的电阻部分,即耗散能量的部分往往可以忽略不计,即上式中的R和G为0,近似为无损传输线。对于无损传输线,阻抗表达式可以表示为(如图2b所示):
特性阻抗是汽车数据线缆非常重要的参数之一,优异的性能离不开阻抗的精确控制。而我们通常所说的阻抗控制,就是为了让传输线尽量均匀,减小反射,控制的就是特性阻抗。
由上面介绍可以知道,特性阻抗的概念是基于两个及以上的导体,因此需要有良好且完整的参考平面作为回流路径,我们要避免参考平面被割裂出现跨分割,这可能会导致阻抗不连续,出现反射(如图3所示)。
图3 信号传输路径示意图
这就好比是你在路面上骑车,路面越平,骑的就越快;如果路面有点小坑,就会很颠簸,速度就会降下来;所以对于高速信号,良好的阻抗控制至关重要(如图4所示)。
汽车数据线缆在研发/设计验证、生产测试、品质管理等应用场景,都需要对产品的特性阻抗进行测试,因此,一套快速、准确、标准的测试方案无疑可以极大的提升测试效率。
关于特性阻抗的测试,有以下三种方式:
1)用TDR法测阻抗
早在60年代就产生了时域反射计(TDR)技术。该技术包括产生沿传输线传播的时间阶跃电压。用示波器检测来自阻抗的反射,测量输入电压与反射电压比,从而计算不连续的阻抗(如图示5所示)。
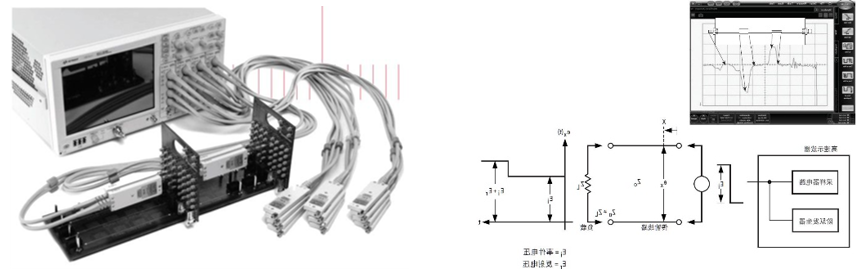
图5 TDR测试设备以及原理图
2)用网络分析仪测输入阻抗
网络分析仪测量测试端口上的输入阻抗(如图6所示)。通常这并非电缆的特性阻抗。如果电缆的电气长度很长,输入阻抗就是电缆的特性阻抗。
图6 网络分析仪测试设备
3)用LCR表测阻抗
可用所谓“开路短路”法测量低频特性阻抗(如图7所示)。在仍可看成是集总元件的最长电缆,通常为1/10波长的电缆上测量开路和短路阻抗。两次测量结果之积的平方根即为特性阻抗。这项技术的缺点是精度低。开路和短路测量可能超出网络分析仪的合理精度。更好的方法是用网络分析仪测量开路和短路阻抗,由于使用电流电压技术而能测量很宽的阻抗范围。
汽车数据线缆中经常看到各种阻抗的电缆,有50Ω、75Ω、90Ω、100Ω、120Ω等,各种应用场景如下:
1)视频信号线阻抗控制为:75Ω。
2)USB信号线差分阻抗为:90Ω。
3)以太网差分信号线差分阻抗为:100Ω。
4)RS422、RS485、CAN差分信号的差分阻抗为:120Ω
这些阻抗控制数值是如何确定的?我们选择一个同轴线的50Ω特征阻抗和双绞线100Ω的差分阻抗做一下简介。
① 同轴线50Ω阻抗
同轴线选择50Ω作为高频特征阻抗匹配是基于功率容量、抗击穿电压和衰减之间的综合考虑的结果,如下图,插入损耗最小,约为77Ω。另一方面,如果绘制最大功率传输与特征阻抗的关系曲线,则最大功率约为30Ω。
图8 50Ω阻抗示意图
当最大功率传输时,特征阻抗值为30Ω,而理论上最小衰减(损耗)的特征阻抗为77.5Ω。在传输功率和最小衰减两个值之间寻找矛盾平衡点,选择传输线的阻抗值为50Ω(如图8所示)。
另一方面,当在较长的同轴电缆(如电缆或卫星电视)中要求最小损耗时,对功率传输没有过高要求时,因此在这些系统中使用了阻抗为75Ω电缆和连接器。
② 差分线100Ω阻抗
单端做匹配时是50Ω阻抗,我们已经了解,那么差分线为什么是100Ω呢?如何来理解这个事情?
如下图9中的差分线,我们单独对每根传输线并联一个Z(这里假设50Ω)的特征阻抗到地。
图9 100Ω阻抗示意图
图中其实已经比较直观的表明了:
因为:I1 = -I2
所以:事实上没有电流通过地到这两个Z,也就是说可以把他们合并成为一个整体,如上图的右边红色部分,其大小为2Z,这就是差分阻抗是100Ω的原因。
实际上,如果这两个传输线之间的间隔太近,他们之间是存在耦合的,正因为这种耦合的存在,每根线上的的阻抗并不是Z 。具体的推理过程这里就不详述了,我们假设耦合系数是k,所以实际上的阻抗值应该是:Z = 2Z(1-k)。
COPYRIGHT © 深圳市展晟自动化科技有限公司 版权所有 粤ICP备18086068号